Introduction
Whether it is for a half-wave dipole or an end-fed half-wave antenna, sooner or later we will have to prune one of these antennas to the correct length. Most of us are accustomed to trial-end error when it comes to tuning a dipole, but there are better ways to do it [1]. This paper describes three methods for your consideration. All of the formulas for the techniques shown may be entered into an Excel spreadsheet. If you do not have Excel on your computer and you have access to Google, you can use Google Sheets [2]. If you have Windows on your computer and have registered, then you can log into your Windows account and use Excel for free at office.com [3]. All three computation methods described may be entered onto a single spreadsheet, as in Figure 1, or entered onto separate tabs. All three techniques will produce the same answers. Most everyone owns a smartphone, so you can bring your spreadsheet app to the yard with you.
Directions for Loading the Spreadsheet
Figure 1 lists the spreadsheet formulas in Column D. Type these formulas over into Column B. Begin typing in Row 8, Column B. You must type an equal sign in front of every formula for the sheet to work. Once the formulas have been entered, enter the variables in the green cells in Column B. It is a good idea to lock the gray cells to protect the formulas from being over-typed. Then, protect the entire sheet so that the only cells open for data entry will be the green cells in Column B. If you click on Figure 1, it will open into a new window for easier viewing.
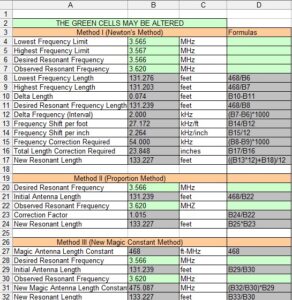
Figure 1. Sample Spreadsheet. Any one of the three methods or all three may be entered onto a single spreadsheet, or onto multiple spreadsheet tabs. A spreadsheet app on your smartphone is an easy way to carry the calculator to the field.
Descriptions of the Methods Used
Method I – Newton’s Method
The first method is one invented by Isaac Newton, but not for antennas. Newton was working with what we now call differential calculus in the late 17th century, which helps to put his genius into perspective. These days, we learn this technique in the first few weeks of calculus in high school. If we use the familiar formula to calculate the length of the dipole at a frequency just above and just below the desired frequency we can get a frequency differential.
If we subtract the two lengths, we get a length differential. By dividing the frequency differential by the length differential, we arrive at the number of kHz the resonant frequency moves per unit of length pruned. If we choose a very narrow frequency interval around our desired frequency, this technique becomes very precise. It’s a kind of sensitivity analysis. We move something a little bit and something else changes a little bit. That’s a hint as to what calculus is all about.
Method II – Proportional Method
The second method, which we call the proportion method, uses the familiar dipole length formula to arrive at the dipole length at a design frequency. In the field, we measure the frequency at which the antenna actually resonates. If we divide the observed frequency by the desired frequency, we arrive at a correction factor by which we multiply the old length to get the new length.
This is the most commonly used method for pruning an antenna.
Method III – New Magic Constant Method
The third and last method is called the “magic constant” method. We all remember that we divide 468 by the frequency in MHz to arrive at the dipole length in feet. The number 468 is what we call the “magic constant.” Suppose we calculate the length of a dipole using the magic constant. In the field, we observe that the dipole resonates at a different frequency. If we divide the observed frequency by the desired frequency, we arrive at a correction factor that can be multiplied by the old magic constant to get a new magic constant.
Then, we use this new magic constant to calculate a new antenna length.
Of the three methods, only the first method is a bit arcane because it uses differential analysis. The latter two are equivalent because they use proportions.
No comments:
Post a Comment